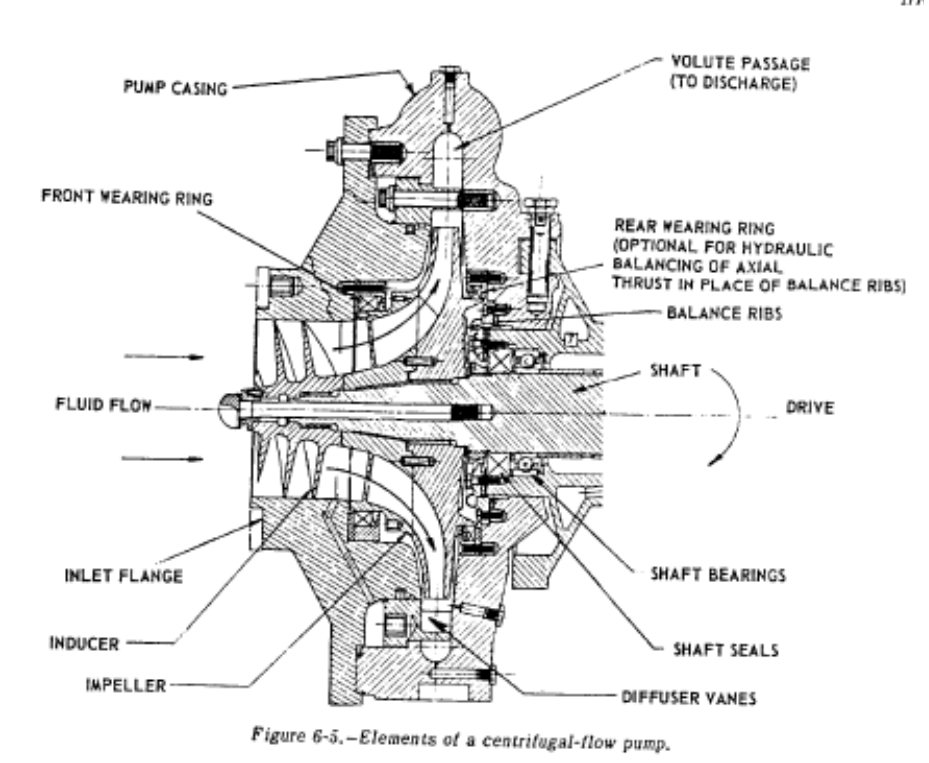
There is currently a fair bit of discussion on the aRocket list about amateur electric and turbine powered pumps, so I thought it would be helpful to go over some basic pump sizing work. Then maybe next post I will show a specific pump impeller design example.
First things first, in order to size a pump you need 4 basic numbers: mass flow rate (mdot), pressure rise (deltaP), fluid density (rho), and RPM. If you don’t have these numbers, then go ahead and make them up now. Now, what we want to calculate is pump specific speed (Ns) and pump power. Pump specific speed is a quasinondimensional number (I’m using English units for Ns and bastard for elsewhere – sorry metric folks!) that should help us identify the pump type and geometry that we should be using and power is useful in selecting our driving motor.
Step 1: calculate volumetric flow rate in GPM
GPM = mdot (kg / s) / rho (kg / m^3) * 60 * 264
Step 2: Calculate head rise
Head rise (ft) = deltaP (psi) / rho (kg / m^3) * 144 / (2.205 * 0.305^3)
Step 3: Calculate specific speed
Ns = RPM * 1000 * GPM^0.5 / Head^0.75
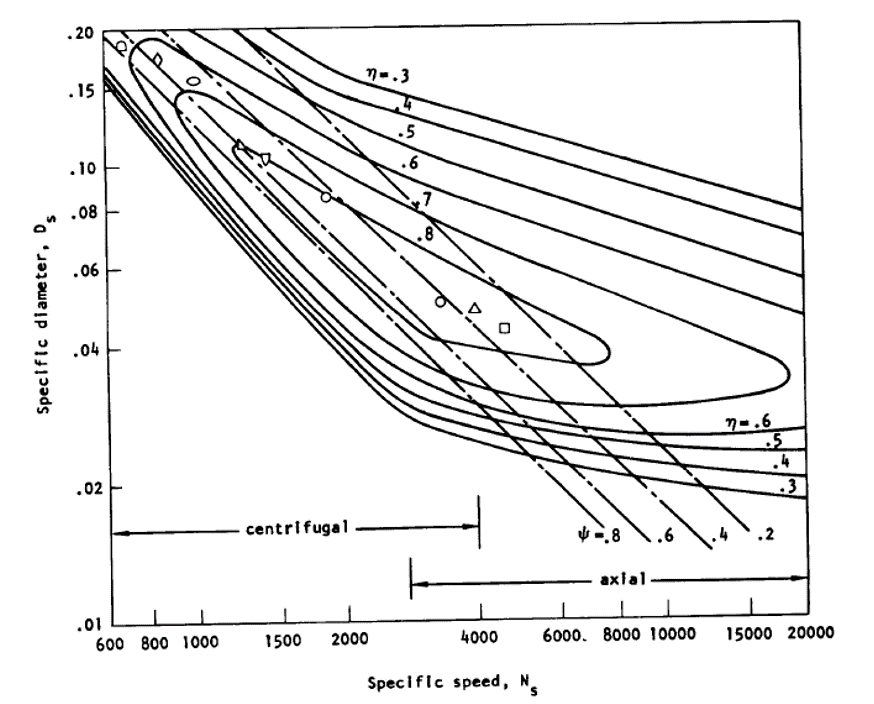
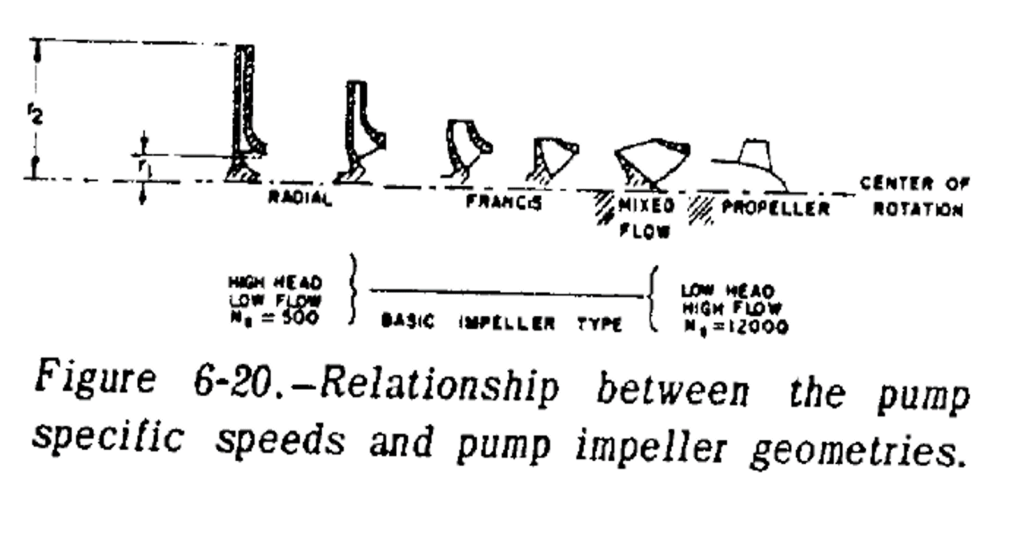
And you should get a number between ~200 and 20,000. You then take the number and compare it to the plot below to choose an appropriate pump type. Radial pumps with around an Ns of 1000 and axial pumps with NS of ~10000 are probably the easiest pumps for an amateur to get up and running. In our case, we would rather do the radial because we need the pressure rise.
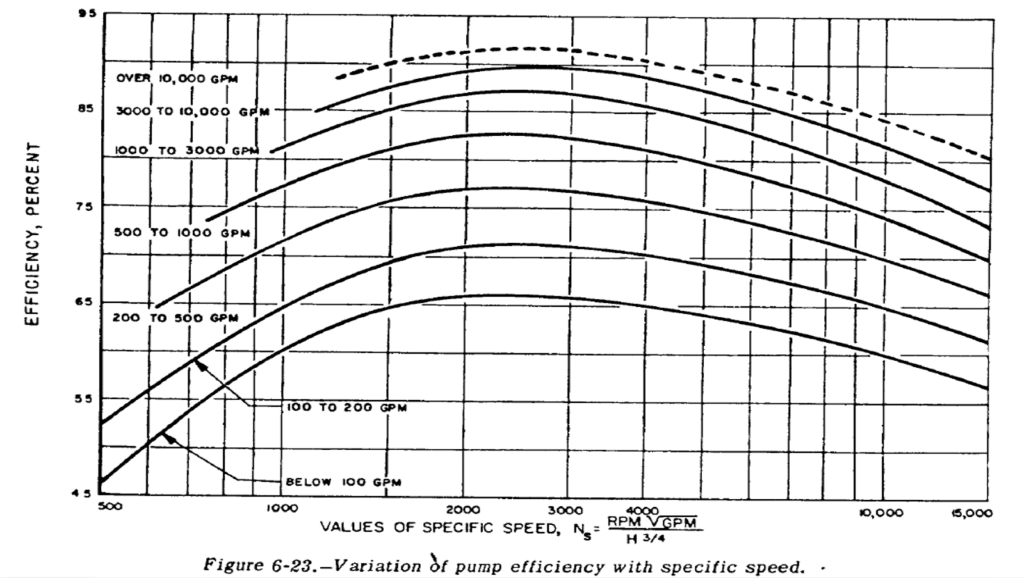
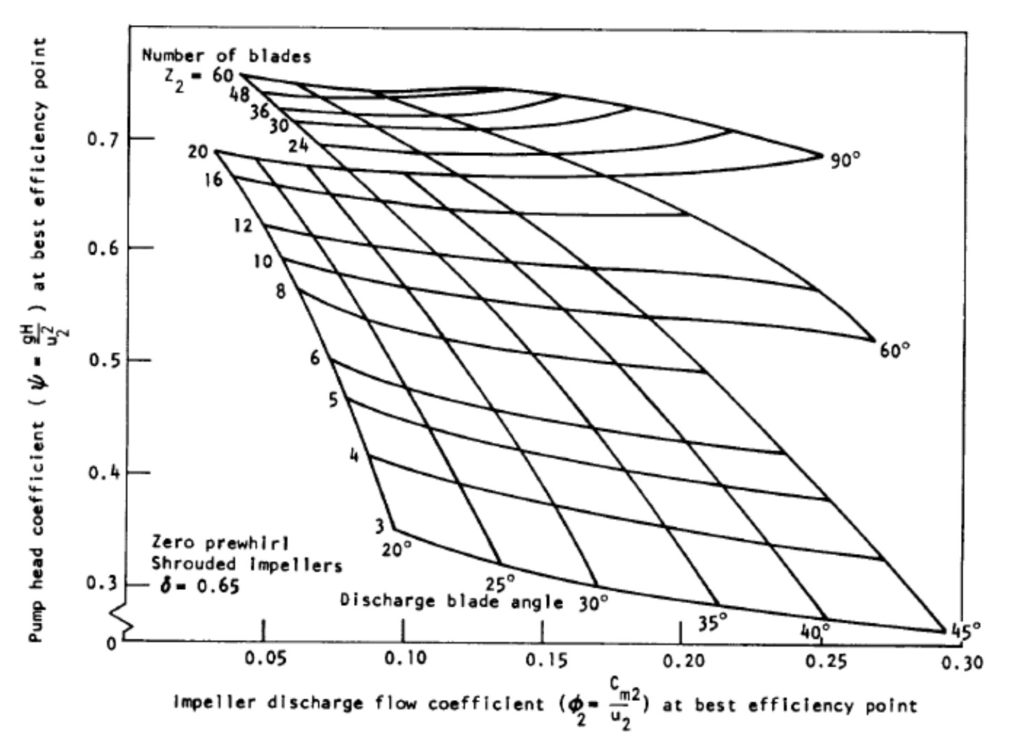
Now, to calculate pump power, we need efficiency; luckily for us, there is a handy chart for that, also from SP-125. Take your GPM and Ns and you get an efficiency. Pretty easy, right? Well, for an amateur, I would say knock off an extra 10% and, for a damn good pro, you might get an extra 10% as these are just standard values. If you don’t like your efficiency, modify your pressure rise or RPM.
You can see that with any pump for a rocket under 100 GPM, or ~10 klbf, you really want Ns up to 1500-4000 for any sort of efficiency.
Now to calculate power.
Step 1: Fluid Power
Power_Shaft (Watts) = Mdot (kg/s) * 9.8 m/s * Head (ft) / 3.28 / Pump_Efficiency
That is the power that you reed to drive the impeller. If you assume an extra 10% power for bearings and seals, you have your pump roughed out.